---

Głównie chodzi mi o wytłumaczenie tej zasady w zadaniach. Kompletnie tego nie łapię. Dla przykładu zadanie zrobione. Proszę o wytłumaczenie co z czego, jak, dlaczego ;p

Z działa o masie 5 ton wystrzelono pocisk ważący 20 kg, z prędkością 400 m/s. Oblicz prędkość odrzutu działa.

md = 5t = 1000kg
mp = 20kg
vp = 400 m/s
vd = ?

1. Przed wystrzałem
Pu1 = 0
2. Po wystrzale
Pu2 = mp *(razy) vp - md * vd
Pu2 = Pu2
mp*vp-md*vd = 0
-md *vd= -mp * vp / :(-md)

vd = mp * vp : (pod kreską ułamkową) md = 20 * 400 : (pod kreską) 5000 = 8 : (pod kreską) 5 = 1.6

---

Jak widać, pęd przed wystrzałem był równy 0, dlatego po wystrzale pęd układu musi wynieść 0. Zarówno działo jak i pocisk po wystrzale uzyskują jednakowe pędy, ale ich zwroty są przeciwne (inaczej ich suma nie była by równa 0). Ponieważ oba obiekty bardzo mocno różnią się masami, więc żeby ich pędy były równe, ich prędkość też muszą być różne.W zasadzie zadanie to zwykłe podstawienie do wzoru z jednym przekształceniem, dlatego ciężko coś i tu dalej wyjaśniać. No i na przyszłość przydałaby się obróbka w Excelu, ale chyba i tak na forum to nic nie da...

---

Podobne zadania my teraz wykonujemy na lekcjach. Tyle, że zadanie samo się zgadza, gorzej z tym przykładem... My mamy jeszcze do tego MJ, a więc jeśli o to chodzi, to wytłumaczę ;>

---

Najpierw trzeba sobie wyobrazić sytuację... Najlepiej to zrobić za pomocą rysunku



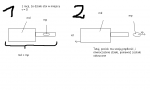
- w pierwszej sytuacji działo stoi w miejscu i ma masę md + mp, ponieważ pocisk jest w środku i mają taką samą prędkość (czyli akurat 0), więc normalnie ich pęd można obliczyć za pomocą: v * (md + mp), a to się równa 0, ponieważ jeżeli coś mnożymy przez zero (w naszym przypadku prędkość) to wynik jest równy zero. Teraz sytuacja druga. Po wyrzuceniu pocisku, działo odsuwa się do tyłu (zawsze tak jest, mamy z tym do czynienia np. w busie, jak nagle zahamuje, to wtedy lecimy do przodu). Tak więc, obydwa ciała mają prędkość, ale nie taką samą i liczymy ich pęd, czyli nasze p2. I tak:
pęd działa wynosi ze wzoru: md * vd
pęd pocisku wynosi (też ze wzoru): mp * vp
Następnie pęd całego układu nr 2 wynosi Pp - Pd
Następnie korzystamy z zasady zachowania pędu:
p1 = p2
I podstawiamy:
v * (m1 + m2) = mp*vp - md*vd
Jak wcześniej ustaliliśmy p1 = 0
a więc:
0 = mp*vp - md*vd
Teraz to są obliczenia matematyczne - wyobraź sobie, że vd jest zwykłym x i poprzenoś tak, żeby ten x był sam po jednej stronie, czyli nam wychodzi:
vd (x) = mp*vp/md
I podstawiamy i mamy wynik...

---

Dzięki bardzo :) Dostałam 4 z tego co pamiętam!!111 <chwali się bezczelnie>

---

Bardzo się cieszę, że dostałaś 4 z fizyki, a odpowiedzi tu zawarte pomogły Ci w tym. Teraz jednak zachowując zasady pędu, muszę go błyskawicznie zamknąć.